how to find standard deviation by looking at a graph

Standard-Deviation-Examples

Introduction to Standard Deviation Examples

There are ample examples of standard deviations. Standard deviation is the measure of the dispersion of the dataset, i.e., how to spread out the numbers are. It is useful for comparing the different sets of data that might have the same mean but a different range. The following different Standard deviation example gives an understanding about the most common type of situations where the Standard deviation is calculated and how one can calculate the same.

Examples of Standard Deviation

Below are the examples of the Standard Deviation

Standard Deviation – Example #1

The stock of Company Z sells for $ 50 per share, and the same offer the following payoffs for the next year:

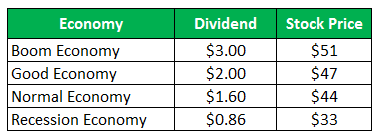
Standard Deviation Examples-1

Calculate the Standard deviation when all the four scenarios are given are equally likely.

Solution:

Calculations of Holding Period Return (HPR) is as follows –

Formula of HPR

HPR = ((End of Period Value – Original Value) + Income) / Original Value) * 100

For Boom Economy

HPR (Boom) = ((51-50) + 3)/50 = 8.00%
HPR (Good) = ((47-50) + 2)/50 = -2.00%
HPR (Normal) = ((44-50) + 1.60)/50 = -8.80%
HPR (Recession) = ((33-50) + 0.86)/50 = -32.28%

Calculation of Expected Return

Since all the scenarios are equally likely, so the probability of all will be ¼

The formula of Expected Return

Expected Return = (Probability of Boom * Return from Boom) + (Probability of Good * Return from Good) + (Probability of Normal * Return from Normal) + (Probability of Recession * Return from Recession)

Expected Return = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8.80 %) + (1/4 x -32.28 %)
Expected Return = -8.77 %

Calculation of Standard Deviation

Formula of Variance

Variance = [Probability of Boom * (Return from Boom – Total Expected Return) ^2] + [Probability of Good * (Return from Good – Total Expected Return) ^2] + [Probability of Normal * (Return from Normal – Total Expected Return) ²] + [Probability of Recession * (Return from Recession –Total Expected Return) ^2]

Variance = 1/4 (8 – (-8.77))²+ 1/4 (-2 – (-8.77))²+ 1/4 (-8.80 – (-8.77))²+ 1/4 (-32.28 – (-8.77))²
Variance = 219.95

The formula of Standard Deviation

Standard Deviation will be Square Root of Variance

Standard Deviation = √Variance

Standard Deviation= √219.95
Standard Deviation = 14.83%

Standard Deviation Example – 2

Standard deviation in the case of two companies in the portfolio

The common stock of Company A sells for $ 28 per share and the same offers following payoffs for the next year

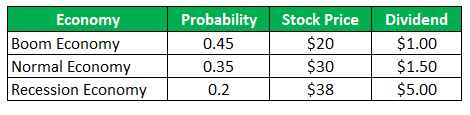
Examples-2

The common stock of Company B sells for $ 93 per share and the same offers following payoffs for the next year:

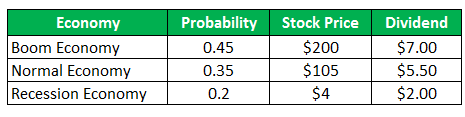
Standard Deviation Examples-2.1

(a) Calculate the standard deviation of Company A

(b) Calculate the standard deviation of Company B

(c) Calculate the standard deviation of the portfolio if half of the investment is done in Company A and the rest half in Company B

Solution:

For Company A

Calculations of Holding Period Return (HPR)

Formula of HPR

HPR = ((End of Period Value – Original Value) + Income) / Original Value) * 100

HPR (boom) = ((20-28) + 1)/28 = -25.00%
HPR (Normal) = ((30-28) + 1.50/28 = 12.50%
HPR (Recession) = ((38-28) + 5)/28 = 53.57%

Calculation of Expected Return of Company A

Formula of Expected Return

Expected Return = (Probability of Boom * Return from Boom) + (Probability of Normal * Return from Normal) + (Probability of Recession * Return from Recession)

Expected Return= (0.45 x -25.00%) + (0.35 x 12.50%) + (0.20 x 53.57%)
Expected Return = 3.84%

Calculation of Standard Deviation Company A

Formula of Variance

Variance=[Probability of Boom * (Return from Boom – Total Expected Return) ^2] + [Probability of Normal * (Return from Normal – Total Expected Return) ²] + [Probability of Recession * (Return from Recession – Total Expected Return) ^2]

Variance= 0.45(-25.00 – (3.84))²+ 0.35 (12.50 – (3.84))²+ 0.20 (53.57 – (3.84))²
Variance= 895.15

The formula of Standard Deviation

Standard Deviation will be Square Root of Variance

Standard Deviation = √Variance

Standard Deviation = √895.15
Standard Deviation = 29.92%

For Company B

Calculations of Holding Period Return (HPR)

Formula of HPR

HPR = ((End of Period Value – Original Value) + Income) / Original Value) * 100

HPR (Boom) = ((200-93)+7)/93 = 122.58%
HPR (Normal) = ((105-93)+5.50/93 = 18.82%
HPR (Recession) = ((4-93)+2)/93 = -93.55%

Calculation of Expected Return

Formula of Expected Return

Expected Return=(Probability of Boom * Return from Boom) + (Probability of Normal * Return from Normal) + (Probability of Recession * Return from Recession)

Expected Return= (0.45x 122.58%) + (0.35 x 18.82%) + (0.20 x -93.55%)
Expected Return = 43.04%

Calculation of Standard Deviation

Formula of Variance

Variance= 0.45 (122.58– (43.04))²+ 0.35 (18.82– (43.04))²+ 0.20 (-93.55– (43.04))²
Variance= 6783.65

The formula of Standard Deviation

Standard Deviation will be Square Root of Variance

Standard Deviation = √Variance

Standard Deviation =√6783.65
Standard Deviation = 82.36 %

Calculation of the Expected Return and Standard Deviation of a Portfolio half Invested in Company A and half in Company B.

Standard Deviation of Company A=29.92%

Standard Deviation of Company B=82.36%

Weight of Company A = 0.50

Weight of Company B = 0.50

The formula of Standard Deviation of Portfolio

Standard Deviation of Portfolio = (Weight of Company A * Expected Return of Company A) + ((Weight of Company B * Expected Return of Company B)

Standard Deviation of Portfolio = (0.50 * 29.92) + (0.50 * 82.36)
Standard Deviation of Portfolio= 56.14%

Analysis

The portfolio standard deviation is lower than for either stock's individual because the stocks are diversified in different stocks. Diversification leads to a reduction in the risk unless a perfect correlation exists between returns on portfolio investments.

Conclusion

The standard deviation measures the dispersion of the dataset, which is relative to its mean. It is calculated as the square root of variance. The greater is the standard deviation of the security, the greater will be the variance between each of the prices and the mean, which shows that the price range is large. The above-mentioned examples are some of the examples of Standard deviation in different ways. There are various other examples as well, which shows that Standard deviation can be calculated using other data.